Introduction
In a previous post, I hinted at how to do multiple hypotheses testing, using the ψ-measure. It turns out to be much clearer just using the posterior probabilities. The ψ-measure has a nice intuitive feel for the two-hypothesis case, but becomes convoluted in the multiple hyptheses case. Further, when introducing the application of Bayes theorem for students, I have found it to be clearer to follow the following procedure. We first look at Bayes theorem directly, for N hypotheses:
We then calculate the numerator only, for every possible hypothesis:
calculate the sum of all of these values,
and then normalize
The Octopus, Again
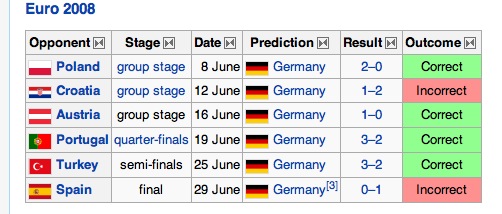
From the Wikipedia article, we have the following data:, which gave us correct=12 out of N=14:
  
The hypotheses that we consider are the following:
H = “Octopus is psychic, and can predict future (sports) events with 90% accuracy” R = “Octopus makes random choices” Y = “chooses flags with big yellow stripes 90% of the time” G = “chooses Germany 90% of the time”
Notice that both models Y and G, give us correct=12 for N=14 (if the “choosing Germany” chooses Spain in the Netherlands match, because of the similarity). The prior for the psychic octopus is, again, the very generous p(H) = 1/100. The two other non-random models should be more likely, before any data, so I take them to be p(Y)=p(G)=1/20. The random model, being the most likely, has the rest of the prior probability, p(R)=0.89.
Now we calculate the numerators:

Sum the values,

and divide. achieving

Thus, the two flag models went from being rare compared to random to being much more likely than random, and certainly much more likely than psychic. Bayes theorem, properly applied, is a quantitative embodiment of Carl Sagan’s famous quote “extraordinary claims require extraordinary evidence”. It is not just that the evidence must be extraordinary (like 999 correct out of 1000), but the evidence must be extraordinary to address all of the, somewhat rare but possible, hypotheses that would come up as much more likely given the initial result. The process of science is to perform experiments to address these alternative hypotheses.



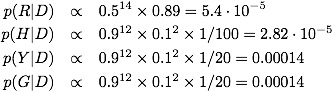

No comments:
Post a Comment