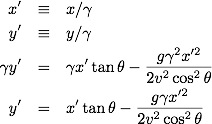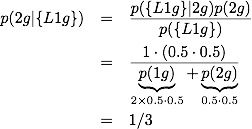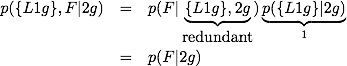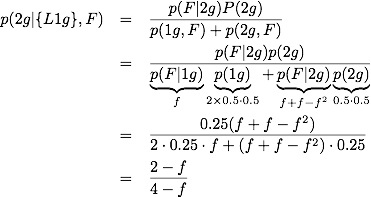Economics

In a post about Ten Principles of Economics, Harvard Professor Greg Mankiw writes a little acrostic device about economics. In addition to things like "Everything has a cost. There is no free lunch. There is always a trade-off." for the "E" in economics, I found this one caught my eye: "One More. Rational people make decisions on the basis of the cost of one more unit (of consumption, of investment, of labor hour, etc.)."

My first thought was, is this really true? Perhaps a real economist will correct me, but I disagree with this statement. From my limited economics knowledge, a rational person makes a decision to maximize the net benefit resulting from that decision, given the information that the person has. This is maximizing the benefits minus the costs, or

Where B(q) is the benefit and C(q) is the cost, and q is a label for the different possible decisions, usually representing the quantity of a particular good that is purchased. To find the maximum (or minimum) we take the derivative and set it to zero:

The decision on the "basis of the cost of one more unit" is referring to dC(q)/dq, or the marginal cost. When the marginal cost equals the marginal benefit, then we are at an optimum (which could be a minimum of the net benefit!).

What I disagree with is that I don't think that people make a decision based on dC(q)/dq, but rather that they make decisions on B(q)-C(q). You might say, "But, hey, those are the same thing!". The distinction I think is found in the correspondence between a model and the real-world. Quantities like the cost of a good, or the benefit of the good, are directly observable and measurable. The marginals, or derivatives, of those same quantities are not directly observable but are inferred from the values of the non-marginal quantities at various values of q.

To make an analogy with physics, think of position and speed. Speed is change of position with time, or the "marginal position" if you will. You measure speed by taking different positions and different times of some object, and calculating speed. You don't measure speed directly. The analogy breaks a bit, because there are ways of inferring speed without position, using the doppler effect, which is how we can measure the speeds of very distant objects without knowing their position.

The question I have is, "Is there a similar way to directly measure the marginal cost, without first knowing the cost of the good?" I don't think that this is possible. First, I think it quite likely that there are cases where B(q)-C(q) is not differentiable, so it makes no sense to think of "just one more" but you can still maximize the quantity. The differentiation is a simplification, a model. Second, the equality of dC(q)/dq to dB(q)/dq occurs at both a minimum and a maximum, and needs to be confirmed if it is truly a maximum by going back to the values of B(q) and C(q). Thus knowledge of "one more" is incomplete. Finally, as stated above, I don't think that the marginals are directly observable, whereas the direct quantities are.

Hopefully an economist will comment and correct, or confirm, what I am saying!

Faith and Science

I was listening to a very nice talk by Ken Miller, from Brown University. He's the Biology professor who testified in the Dover Evolution Trial. The reason that he is involved in cases involving the attack on evolution from the religious right is several-fold, including his knowledge of evolution (even though that is not his main area of expertise) and his widely-used textbook (which was the target of the warning labels in Georgia). Ken Miller keeps a page on evolution and his own webpage with many links, presentation slides, and talk videos. I think the most important reason for his involvement is that he is a self-acknowledged Christian (a Catholic, to be specific). Rather than inviting an expert like Richard Dawkins (who is decidedly anti-religious) to testify, it is much better to invite someone who claims there is no conflict between religion and science. Thus the case can't be cast as a battle between science and religion, and can be seen only as what is appropriate science education.

So in his talk, Ken Miller makes the point that science should inform faith and faith should inform science. He cites Paul Davies, a physicist who has an interest in theism, and whose article "Taking Science on Faith" takes the position that science itself is a faith-based activity. Ken Miller points out, and you can confirm in Paul Davies' article, that there are two tenets in science that are taken on faith:

1. the universe is ultimately knowable and understandable
   
2. knowledge is better than ignorance
   

At first I thought that one perhaps should call these axioms, more like mathematics, and not "faith" because something in me felt that these two ideas were different somehow than the belief in God. Then, I realized, that they are different fundamentally and faith, or even axioms, is entirely wrong.

The first idea, that the universe is knowable, needs to be a bit more specific: what does it mean to be knowable? Prior to 1900, it was believed that the pieces of a physical model, such as the force of gravity, or the electric and magnetic fields of Maxwell were "real": there was one-to-one correspondence between the model components and things in the real world. Thus, it was believed, that knowing the model you would know nature. After 1900, with the advent of quantum mechanics, physical models were evaluated based on their predictive value: those models that predicted well were good models. It was not believed that there was necessarily a correspondence between the model components and the real components in nature. Aspects of the model, such as the wave function, were not believed to be real but simply useful in making predictions. To know the world is to be able to predict what would happen.

Let's say we replace "understandable" with "predictable", a replacement which I think makes practical sense (how else would you determine that you understand something?), and is directly in line with modern physical thinking. Doing this, then tenet (1) ceases to be an axiom, or something we take on faith, but is observable. If the universe is unpredictable, then all attempts at making prediction will fail. This is not what we observe at all. Surely there are still things that are unpredictable, such as the simultaneous value of the position and momentum of the electron, or the positions of every molecule of air in this room, but even there we can make specific predictions about average quantities or the values of other variables of interest. Practically, the universe has demonstrated itself to be understandable, on the whole. This is not a matter of faith!

The second tenet (2) I would wager is too vague. What does "better" mean? Better for whom, or for what? Psychologically, one might argue something akin to "ignorance is bliss", and there might be something to that. If we define, however, "better" to be higher standard of living (longer, healthier, more free life) then knowledge can be argued to have a demonstrable benefit over ignorance. The results of science has doubled the life expectancy in the past 100 years, and has allowed us to live more free and healthy lives. The thousands of years of faith before that cannot say as much. As Carl Sagan says, science delivers the goods. Is there any convincing argument that ignorance is better, or that we really can't decide which is better? Is there a preferable definition of "better"?

A couple of interesting videos

With the advent of computer technology, it can be challenging to distinguish fact from fiction.  Both of the videos below are, in my opinion, strikingly real but are both fake (and funny!). Critical thinking skills are a must!

Creativity, Science, and the Brain

In my post about Bruce Hood's interview I said there wasn't anything I disagreed with. After re-listening to it, I find my position is a bit more nuanced. I'd still like to look more closely at the experiments he cites to see if there is anything there that addresses my concerns, like the difference between believing in an external essence of an object versus experiencing the memories that an object elicits. In this post I want to address something that both Bruce and Tom dance around during the interview: the positive aspects of superstition.

Tom tries to tie Bruce down concerning the bad aspects of superstition, citing witch burning and crusades. Bruce refuses to acknowledge superstition as a bad thing, and simply states that superstitious thinking, combined with economic factors and political motivation, can lead to such bad consequences. He further states that intuitive thinking is essential for science. Science doesn't just creep forward in small steps, but is also driven by the intuitive leaps of the scientists. Our ability to see patterns leads us to the patterns we have accumulated in scientific knowledge, and this ability is a consequence of natural selection.

Bruce Hood further talks about unconscious reasoning, such as the dream of Friedrich Kekulé and the structure of benzene, and solving problems while you sleep or are taking a break. I myself have solved some problems this way, and many of the interesting physics problems that I have used in my teaching have come, seemingly randomly, while doing mundane things like raking leaves or taking a shower. Although he states that he is an atheist, and is a scientist, I don't think he goes far enough in supporting science. In this way, his omission leads to the sense that he is a bit too supportive of the poor thinking associated with superstition. He points out that much of it is not factually correct, but I think he misses a big point in his exposition (one that I am quite confident he'd agree with).

Carl Sagan put it this way:

At the heart of science is an essential balance between two seemingly contradictory attitudes—an openness to new ideas, no matter how bizarre or counterintuitive they may be, and the most ruthless skeptical scrutiny of all ideas, old and new. This is how deep truths are winnowed from deep nonsense.

It is this sentiment that is missing from the interview, and would have cleared up many of the questions. Yes, we are all programmed (via natural selection) to be superstitious, to see patterns that may or may not really exist, to attribute properties to objects that may or may not be real. Science works by starting with that, and skeptically testing every pattern to see if it is real. It is only the ones that can stand up to skeptical scrutiny that we can trust.

Thus, Bruce's "super-sense" is the starting point, the intuition which leads to "crazy" ideas, out-of-the-box solutions. Skepticism, open information, and honesty reduce the many possible ideas down to the ones that are true. In some way, this is like the process of natural selection: the "random" element in evolution (mutation, crossover, etc...) leads to variation, and natural selection works on that variation to produce the (far fewer) solutions that are optimal for the various ecological niches. In science, intuition gives us the variation, and skepticism and careful observation work on that variation to produce the (far fewer) solutions that are true.

Finally, in the fine words of Carl Sagan from his book "A Demon Haunted World" (the best science book for the public I have ever read!):

A physicist has an idea. The more he thinks it through, the more sense it seems to make. He consults the scientific literature. The more he reads, the more promising the idea becomes. Thus prepared, he goes to the laboratory and devises an experiment to test it. The experiment is painstaking. Many possibilities are checked. The accuracy of the measurement is refined, the error bars reduced. He lets the chips fall where they may. He is devoted only to what the experiment teaches. At the end of all this work, through careful experimentation, the idea is found to be worthless. So the physicist discards it, frees his mind from the clutter of error, and moves on to something else.

Believing the unbelieveable

Have a listen to this excellent interview of neuroscientist Bruce Hood. I can't think of a single thing I disagreed with this guy on. I may have more specific to say later, and perhaps I will buy his book.

A teachable moment...lost

So I just watched the Mythbusters episode where they recreate the bus jump from the movie Speed. They do two things: a miniature version and full-scale recreation. In their miniature version they scale down the bus by a factor of 12, very carefully building the model bus as closely as possible. Then they scale down the bridge by the same factor. They then point out that they can't scale down gravity without going to the moon. Technically, that would scale gravity by 1/6, not the required 1/12. You wouldn't even have to go nearly as far as the Moon to achieve this. Since force gravity decreases as the square of the distance away from the Earth (starting at 4000mi, the radius of the Earth), you would only have to go up this high:

compared to the 240,000 mi, that's a real bargain! But this is about 10,000 mi above the Earth, whereas the Hubble is less than 600 mi above the Earth, just to give some perspective.

So, without leaving the Earth, the NASA experts say that one can compensate by going faster. Mythbusters scrawls the analysis on the side of the buss and says "basically, what these hieroglyphics mean is to compensate for the physical impossibility of scaling gravity, the speed of our 1/12 scale bus has to be just over 20 miles per hour". What bothers me most about this is not that they don't really go through the analysis, but that they refer to basic math as hieroglyphics and they give no sense for why going a bit faster would compensate for gravity. I am going to include the full analysis here, but below I will also give a simpler explanation that they could have used, which only includes a small amount of math that would have easily fit on the side of the bus.

Analysis

Their analysis is equivalent to the following: the components of the speed off of a ramped angle are

and the x and y positions versus time are given by the standard motion equations

Here is the critical step. We solve for time, t, and get rid of it in the second equation. This way we have the shape of the entire trajectory in space, without any dependance on time.

or:

Now, what happens to this equation when we scale the distances down by a certain amount?

which is almost the same, except for one factor of gamma over the v² term. Thus, if we replace the speed with

the trajectory of the new version is identical to the old version. Now, remember, that this doesn't include time: the scaled version, going a faster, will reach the destination sooner.

A Clearer Way

I certainly wouldn't expect the television audience to follow that analysis, although I wouldn't mind them showing it anyway (but more explicitly). It's the sort of thing where many would ignore it, but the ones who could understand it would get more out of the show. So let's see if we can put it a bit more clearly. I'd start, first, by scaling down the sizes by a factor of 16 not 12. That way I can take the square root more easily. Then there'd be two more facts about gravity that I would mention

1. gravity doesn't affect motion horizontally
   
2. vertically, if I throw something up at three times the speed, it will go up nine times the height (the square of the speed increase)
   

Scaling down just the size, but not the speed, by a factor of 16 would decrease the time by the same factor of 16. If we scale the speed down by a factor of 4, then three things happen: the height of the trajectory reduces by 16 (item 2 above), the time of flight reduces by a factor of 4, and thus the horizontal distance covered (speed times time) is reduced by a factor of 4x4=16. Notice that in doing so, the object trajectory is scaled in both the vertical and horizontal directions by 16, which is the goal of the scaling.

I think that this is clearer than the way presented by Mythbusters, and should have been covered in this way, or some similar way. It could have have been a good teaching moment!

There once was a girl named Florida (a.k.a Evil problems in probability)

In a previous post I described the Monty Hall problem, and noted that a simulation can often lead to clarity of thinking on tough probability problems. I take another example here, in two steps, and throw analysis and simulation at it and possibly a bit of intuition.

I was first introduced to this problem from Leonard Mlodinow's "The Drunkard's Walk: How Randomness Rules Our Lives" and immediately "fell for the trap". The problem exists in two parts, the first (easy) part followed by the second (hard) part. The easy part is as follows:

Say you know a family has two children, and further that at least one of them is a girl. What is the probability that they have two girls?

An easy way to do this is to list out the possibilities:

• Boy-Girl
  
• Girl-Boy
  
• Girl-Girl
  

so you end up with 1 chance out of 3, or p=0.33. The hard part is the following:

Say you know a family has two children, and further that at least one of them is a girl named Florida. What is the probability that they have two girls?

At first I didn't think it would make any difference. How could knowing the name of the child change the chances for two girls? So I didn't believe the author (at first) that the chances were even, p=0.5, for the family to have two girls. Again we can list off the possibilities:

• Boy-Girl (Florida)
  
• Girl (Florida)-Boy
  
• Girl (Not Florida)-Girl (Florida)
  
• Girl (Florida)-Girl (Not Florida)
  
• Girl (Florida)-Girl (Florida)
  

Since the last point is very rare (two girls named the same rare name?) we can ignore it, and we can also see that there are now two Girl-Girl possibilities with one named Florida, rather than just one, so it essentially gets two votes. Thus, we get p=0.5. Now, when I see something like this I worry. Yes, it's intuitive (once you see it) but I've seen slight-of-hand counting of the possibilities before. I don't trust it unless I can do two things:

1. write a simulation which reproduces it
   
2. show that a formal analysis works for the problem
   

As for the simulation (I post the code below) I get:

Probability for a girl to be named Florida:  0.01
Total number of families with two children:  1000000
999862 girls (0.499931 of children)
249745 both girls (0.249745)
750117 families with girls (0.750117)
249745 both girls (0.332941) given families with girls
10084 families with a girls named florida
4997 both girls (0.495537) given families with girl named florida

The formal analysis gets interesting, because I want to understand how the frequency, f, of the name affects the probability of having two girls. If it is a rare name (f ~ 0) then I should get p=0.5. For a common name (f ~ 1) then I should get p=1/3. Not that with f=1 then the word "name" is a little odd because all girls have it, so one might think of it as a label (like "has a nose"). First some notation:

Applying Bayes theorem to the easy problem, we get:

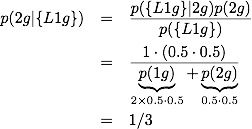
The hard problem is set up like:

It is clear that p({L1g}|2g)=1 whereas p({L1g},F|2g)=1 is not: given that we have 2 girls, we definitely have at least one girl, but we need not have at least one girl named Florida. Breaking the second term up we get

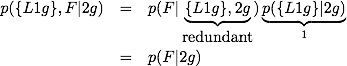
Now we have

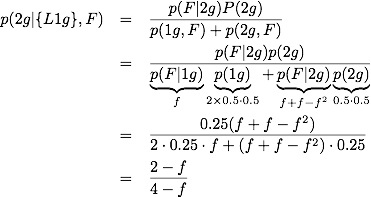
It is easy to check that it has the right limits:

I'm not sure if there is a better way to address this problem, but the analysis and simulation agree, and further we have a very simple form for how the probability depends on the frequency of the known label (e.g. Florida).

Code for simulation

from pylab import *
from numpy import *

# 2 daughter problem

num_families=1000000
num_children_per_family=2

f_girls=0.5
f_florida=0.01
print "Probability for a girl to be named Florida: ",f_florida
print "Total number of families with two children: ",num_families

child_types=['boy','girl']
families=[ (child_types[randint(2)],child_types[randint(2)]) for x in range(num_families)]

names=[]
for f in families:
    
    if f[0]=='boy':
        name1='Bob'
    else:
        name1='Florida' if rand() < f_florida else 'Sarah'
        
    if f[1]=='boy':
        name2='Bob'
    else:
        name2='Florida' if rand()< f_florida and name1!='Florida' else 'Sarah'
        
    names.append( (name1,name2) )
    
# total fraction of children as girls
girls=0
children=0
for f in families:
    for c in f:
        children+=1
        if c=='girl':
            girls+=1
print "%d girls (%f of children)" % (girls,float(girls)/children)

# total fraction of families with both girls
both_girls=0
for f in families:
    if f[0]=='girl' and f[1]=='girl':
        both_girls+=1
print "%d both girls (%f)" % (both_girls,float(both_girls)/num_families)

# total fraction of families with both girls GIVEN that the family has a girl
families_with_girls=[]
for f in families:
    if f[0]=='girl' or f[1]=='girl':
        families_with_girls.append(f)
        
num_families_with_girls=len(families_with_girls)
print "%d families with girls (%f)" % (num_families_with_girls, 
                        float(num_families_with_girls)/num_families)

both_girls=0
for f in families_with_girls:
    if f[0]=='girl' and f[1]=='girl':
        both_girls+=1
print "%d both girls (%f) given families with girls" % (both_girls,
                            float(both_girls)/num_families_with_girls)


# total fraction of families with both girls GIVEN that the family has a girl named florida
families_with_florida=[]
for n,f in zip(names,families):
    if f[0]=='girl' and n[0]=='Florida' or f[1]=='girl' and n[1]=='Florida':
        families_with_florida.append(f)

num_families_with_florida=len(families_with_florida)
print "%d families with a girls named florida" % num_families_with_florida

both_girls=0
for f in families_with_florida:
    if f[0]=='girl' and f[1]=='girl':
        both_girls+=1
print "%d both girls (%f) given families with girl named florida" % (both_girls,
                            float(both_girls)/num_families_with_florida)

Weird associations and the brain

You ever have deja vu? The brain associates many things together, and can often give you the visceral feeling that you've been there before. For several years I have had a very specific deja vu that I have finally tracked down. I found for some reason that when I watched the movie Unbreakable (great movie!) that later in the day I would recall a video game in my distant past called the Legend of Zelda, that I played on our Nintendo game machine. This happened a couple of times, so I felt there was some association that I couldn't quite pick up.

Then I noticed that each time, I was humming the theme song to Zelda during the day, and I finally figured out the association: the musical transitions in the themes are close enough that hearing one, I would continue with the other. The clips are below. If you listen to about 30 seconds of the Unbreakable music, you'll get the theme, and then go back to the Zelda clip. How random! But now I have the satisfaction of a puzzle solved!

• Unbreakable clip
  
• Zelda clip
  

Cool little fact of the day...

Did you know that if you interleave the pages of two phone books, that it is nearly impossible to separate?

For those Mythbusters aficionados this won't be news, but since I don't watch TV I missed this one. I just heard about it yesterday, and didn't believe it. So I did a quick test myself and confirmed it! Very cool!

You can see what mythbusters does with it here (note: it involves tanks):

http://www.youtube.com/watch?v=hOt-D_ee-JE