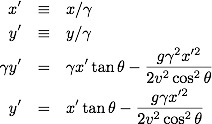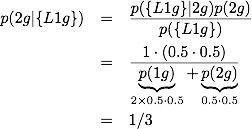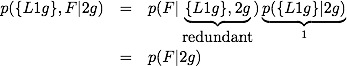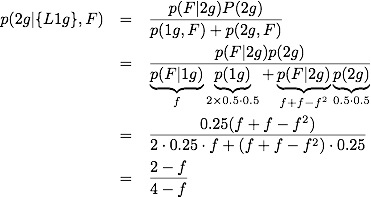In a
previous post I described the Monty Hall problem, and noted that a simulation can often lead to clarity of thinking on tough probability problems. I take another example here, in two steps, and throw analysis and simulation at it and possibly a bit of intuition.
I was first introduced to this problem from Leonard Mlodinow's "The Drunkard's Walk: How Randomness Rules Our Lives" and immediately "fell for the trap". The problem exists in two parts, the first (easy) part followed by the second (hard) part. The easy part is as follows:
Say you know a family has two children, and further that at least one of them is a girl. What is the probability that they have two girls?
An easy way to do this is to list out the possibilities:
- Boy-Girl
- Girl-Boy
- Girl-Girl
so you end up with 1 chance out of 3, or p=0.33. The hard part is the following:
Say you know a family has two children, and further that at least one of them is a girl named Florida. What is the probability that they have two girls?
At first I didn't think it would make any difference.
How could knowing the name of the child change the chances for two girls? So I didn't believe the author (at first) that the chances were even, p=0.5, for the family to have two girls. Again we can list off the possibilities:
- Boy-Girl (Florida)
- Girl (Florida)-Boy
- Girl (Not Florida)-Girl (Florida)
- Girl (Florida)-Girl (Not Florida)
- Girl (Florida)-Girl (Florida)
Since the last point is very rare (two girls named the same rare name?) we can ignore it, and we can also see that there are now two Girl-Girl possibilities with one named Florida, rather than just one, so it essentially gets two votes. Thus, we get p=0.5. Now, when I see something like this I worry. Yes, it's intuitive (once you see it) but I've seen slight-of-hand counting of the possibilities before. I don't trust it unless I can do two things:
- write a simulation which reproduces it
- show that a formal analysis works for the problem
As for the simulation (I post the code below) I get:
Probability for a girl to be named Florida: 0.01
Total number of families with two children: 1000000
999862 girls (0.499931 of children)
249745 both girls (0.249745)
750117 families with girls (0.750117)
249745 both girls (0.332941) given families with girls
10084 families with a girls named florida
4997 both girls (0.495537) given families with girl named florida
The formal analysis gets interesting, because I want to understand how the frequency,
f, of the name affects the probability of having two girls. If it is a rare name (
f ~ 0) then I should get p=0.5. For a common name (
f ~ 1) then I should get p=1/3. Not that with
f=1 then the word "name" is a little odd because all girls have it, so one might think of it as a label (like "has a nose"). First some notation:

Applying Bayes theorem to the easy problem, we get:
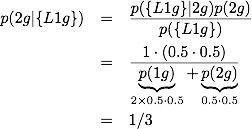
The hard problem is set up like:

It is clear that p({L1g}|2g)=1 whereas p({L1g},F|2g)=1 is not: given that we have 2 girls, we definitely have at least one girl, but we need not have at least one girl named Florida. Breaking the second term up we get
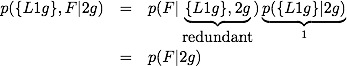
Now we have
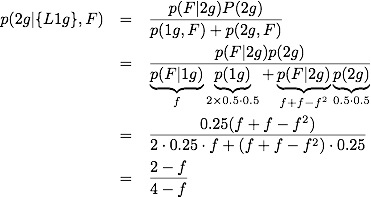
It is easy to check that it has the right limits:

I'm not sure if there is a better way to address this problem, but the analysis and simulation agree, and further we have a very simple form for how the probability depends on the frequency of the known label (e.g. Florida).
Code for simulation
from pylab import *
from numpy import *
# 2 daughter problem
num_families=1000000
num_children_per_family=2
f_girls=0.5
f_florida=0.01
print "Probability for a girl to be named Florida: ",f_florida
print "Total number of families with two children: ",num_families
child_types=['boy','girl']
families=[ (child_types[randint(2)],child_types[randint(2)]) for x in range(num_families)]
names=[]
for f in families:
if f[0]=='boy':
name1='Bob'
else:
name1='Florida' if rand() < f_florida else 'Sarah'
if f[1]=='boy':
name2='Bob'
else:
name2='Florida' if rand()< f_florida and name1!='Florida' else 'Sarah'
names.append( (name1,name2) )
# total fraction of children as girls
girls=0
children=0
for f in families:
for c in f:
children+=1
if c=='girl':
girls+=1
print "%d girls (%f of children)" % (girls,float(girls)/children)
# total fraction of families with both girls
both_girls=0
for f in families:
if f[0]=='girl' and f[1]=='girl':
both_girls+=1
print "%d both girls (%f)" % (both_girls,float(both_girls)/num_families)
# total fraction of families with both girls GIVEN that the family has a girl
families_with_girls=[]
for f in families:
if f[0]=='girl' or f[1]=='girl':
families_with_girls.append(f)
num_families_with_girls=len(families_with_girls)
print "%d families with girls (%f)" % (num_families_with_girls,
float(num_families_with_girls)/num_families)
both_girls=0
for f in families_with_girls:
if f[0]=='girl' and f[1]=='girl':
both_girls+=1
print "%d both girls (%f) given families with girls" % (both_girls,
float(both_girls)/num_families_with_girls)
# total fraction of families with both girls GIVEN that the family has a girl named florida
families_with_florida=[]
for n,f in zip(names,families):
if f[0]=='girl' and n[0]=='Florida' or f[1]=='girl' and n[1]=='Florida':
families_with_florida.append(f)
num_families_with_florida=len(families_with_florida)
print "%d families with a girls named florida" % num_families_with_florida
both_girls=0
for f in families_with_florida:
if f[0]=='girl' and f[1]=='girl':
both_girls+=1
print "%d both girls (%f) given families with girl named florida" % (both_girls,
float(both_girls)/num_families_with_florida)