“I almost bought your discussion until you provided the diagram from Kiehl and Trenberth which is ludicrous. The whole construct here is to create the illusion that the sun cannot heat the earth above minus 18 which is absolute nonsense based on assuming it is valid on geometric grounds to reduce the solar insolation by a factor of 4 then again by the albedo.
If this is valid how then does the surface temperature of the moon reach ~123 C - quoted by NASA.
And how do you explain daytime temperatures on Earth in excess of 50 C as has been recorded ?”
I will focus on the Moon part, just because it is the easiest, but it will be natural to see how to approach this for the Earth as well. First, I must point out the irony of the comment. In trying to defend the claim that the climate models ignore conduction and convection, and focus exclusively on radiation, the comment refers to a system (the Moon) where there is no atmosphere and thus no conduction (except within the ground itself) or convection! Second I have to wonder about how stupid the commenter thinks NASA is. Do they really think that scientists would consider models that are flagrantly in conflict with the most basic observation about the Moon’s surface (i.e. its temperature extremes)? Do they really think that scientists would come up with a calculation that Moon can’t achieve temperatures above, say, -18 C and then stare at 100 C temperature measurements and just leave the calculation as is for decades? Let’s consider how one would develop a model of the surface temperature of the Moon, and it will answer the objections raised in the comment, as well as outline how real science actually progresses.
The Average Blackbody Model
We start with a very simple model of a spherical body out in space receiving input from the Sun to the tune of 1400 W/m2. At the same time, the spherical body emits radiation with a power per square meter dependent on T4 (i.e. the blackbody law).
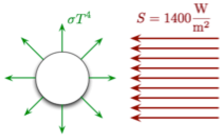
Notice that in this very simple model we are assuming several things:
- that the conduction within the body is instantaneous, thus the temperature of the body is uniform, and the output energy is uniform.
- the body is not rotating, so the radiation it is receiving is constant
- there is no atmosphere, thus no conduction or convection outside of the solid body
- the albedo is the average albedo of the Moon, or a=0.14. Thus this object absorbs 86% of the radiation coming in
The total energy out of the body would be the blackbody term shown, multiplied by the total surface area of the sphere: the radiation is outward in all directions. The incoming radiation, however, strikes only one side. Further, it strikes at different angles. Applying calculus one finds that the effective area is simply the cross-sectional area of the sphere, or the area of a circle the same size as the sphere.
We can then write down the change in the temperature, which depends on the material (the mass and specific heat), given the net energy input to the body. I’ll call this dependency K...its exact value, although calculable, will not be important in the model except qualitatively. We then have
When the “energy in” is greater than “energy out”, the temperature increases. When “energy in” is less than “energy out” the temperature decreases. Once it reaches equilibrium, temperature remains constant. What constant? That would be when dT/dt=0, or...

If we look up the values for the actual Moon we get the following:

So our model is not too bad, for the average value, but it could probably be improved. So, now back to the comment which motivated this all:
“If this is valid how then does the surface temperature of the moon reach ~123 C - quoted by NASA.”
The bottom line here is that, if there is an observation that is in conflict with a model, one of the assumptions of the model is probably incorrect, or perhaps you’re comparing the wrong observations to the model. We assumed that the object has a uniform temperature but we know from the 3 data points above (the min, max and mean temperatures) that this is not true! Essentially our model didn’t even attempt to describe temperature variations on the surface, so it comes as no surprise that it is not consistent with them. Many times theorists will use a model, with known deficiencies, because they are interested in different questions: perhaps we are only interested in the average value, and what happens from that average value? In that case, it doesn’t make a lot of sense to include complexities that will be averaged out anyway when we want to answer our question.
To miss this point is to miss the entire process of comparing theory with experiment. It turns out, however, in this case we can make a few simple modifications to explore some of the temperature variation.
The Infinitely Slow Surface-Conduction Model
We use the same assumptions as before, with one modification (in bold):
- that the conduction within the body takes an infinite amount of time (i.e. no surface conduction at all). Thus, each patch of surface acts as its own independent object
- the body is not rotating, so the radiation it is receiving is constant
- there is no atmosphere, thus no conduction or convection outside of the solid body
- the albedo is the average albedo of the Moon, or a=0.14. Thus this object absorbs 86% of the radiation coming in
Near-side patch
Imagine a patch of surface 1 square meter, with the same albedo as the Moon (i.e. absorbing 86%), and a combined mass and specific heat summarized by a constant K’. The energy equation then becomes
at equilibrium we thus have

which again, is reasonably close to the real value. Notice that all we had to do is change the conduction assumption to get surface temperature variation. If you’re concerned that the maximum temperature predicted is lower than the observed, notice that I am using the average albedo of the Moon. There are parts of the Moon’s surface with a lower albedo, and will thus get hotter as a result.
Far-side patch
Now imagine a patch of surface 1 square meter, with the same albedo as the Moon (i.e. absorbing 86%), and a combined mass and specific heat summarized by a constant K’ but with no sunlight at all coming in. The energy equation then becomes
The only equilibrium value for this is T=0. If no energy is coming in, and we have energy going out, the object will keep cooling. So in this model we have the near side T=380 K and the far side T=0 K, at equilibrium.
Although the model is clearly wrong, it demonstrates one thing: you can easily get temperatures above and below the average-model calculation simply by having not all parts of the surface heated equally, and some non-zero time of energy “communication” (i.e. surface conduction or, if you have an atmosphere, conduction and convection with the atmosphere) between the parts. The extreme version calculated here simply demonstrates the effect and is not meant to be realistic.
Adding a Few More Complexities - Qualitative Discussion
We now modify the assumptions as follows
- that the conduction within the body takes a finite, non-zero, amount of time
- the body rotates once every 28 days, like the Moon
- there is no atmosphere, thus no conduction or convection outside of the solid body
- the albedo is the average albedo of the Moon, or a=0.14. Thus this object absorbs 86% of the radiation coming in
- the maximum temperature predicted will be a bit lower than the no-conduction model. This is primarily because the moon rotates the near-side patch out of the the most direct sunlight relatively quickly. If the surface conduction is on the order of minutes, this will make little or no difference. If it is around hours to days then it will. In fact, one could use this difference to help determine the time constant (related to the constant K’) for the surface of the Moon
- the minimum temperature predicted will be higher than the T=0 predicted from the no-conduction model. This is both because the moon rotates the far-side patch out of the dark, and that energy from the previously warmed surface will conduct to the far-side patch.
Conclusions
This all started when I criticized someone’s commentary on climate models, where they claimed that the models exclude thermal conduction and convection, and thus the focus on greenhouse gasses was entirely inappropriate. A further comment claimed that these models put an explicit maximum temperature achievable when they calculate the surface temperature of an object from blackbody equations. The comment further criticized my use of the average model summary for the Earth for this reason.
Notice the procedure we employed to model the system, and address these concerns. We started with a very simple globally averaged model, and got an interesting temperature value similar to the data. We then added a few complexities, such a differential heating, and noticed how this gives a range of temperatures on the surface. We also noticed that the range was half right (half wrong?): the maximum was good, but the minimum was terrible. Adding rotation and non-zero conduction time gives some dynamics and can achieve reasonably close agreement. A more detailed implementation of the local albedo fixes the small errors, especially on the top end. By using this procedure, we can see exactly which parts of our model give which parts of the result. It also shows which parts of the model give the biggest effect, and which are there for small adjustments.
All that is needed to go beyond the average model, and achieve temperature well above the average, is to include differential heating of the surface and some non-zero time of energy “communication”. Once you heat different parts in different ways, and add rotations and time-delays of conductions, you get some interesting dynamics around the average, going both above and below the average. The average calculation is still useful, if you’re not interested in short-term dynamics. It is further useful as a pedagogical tool, because it is a lot simpler. Thus it is not “ludicrous” to use the diagram from Kiehl and Trenberth, as long as one is aware that this is a globally averaged model. If you attempt to infer things well beyond the point of the model, then do not criticize the model - criticize your comparison, and look for a more detailed model that addresses the questions that you’re interested in.